If you should you be wondering about the whats and the hows of math heuristic methods, then you have come to the right place. In this article, we will be sharing with you 12 methods that can help solve mathematical sums the heuristic way.
If you haven’t yet known about Singapore Math or the Singapore Math Method, it is an educational approach to learning or teaching mathematics that originated from the Singapore syllabus and the teaching approaches used in Singapore schools. It emphasizes a problem-solving focus and the development of critical thinking skills which incorporate learning mathematics skills with math heuristic methods.
Singapore Math Curriculum
In the Singapore Math curriculum, the heuristic approach refers to problem-solving strategies or techniques that students can use to solve mathematical problems. These heuristics are designed to help students strategize and solve problems systematically and efficiently. They provide a structured framework for students to think through and to analyze the given problems, thus encouraging them to think creatively, logically and independently.
Learning math heuristic methods is essential especially when solving the difficult word problems in Singapore MOE schools’ Mathematics Paper 2. In order to perform their best, top students who have an understanding of such methods are able to have the advantage of solving the more challenging sums that appear at the end of the paper. It is also crucial that students pick up some of these math heuristic methods from young.
At Seriously Addictively Math – HOUGANG (S.A.M. Hougang), we show these strategies at early ages, at levels they can understand and be challenged so that the math heuristic methods do not baffle them when such solution methods will be offered to them at later years.
We adapt 12 commonly taught Singapore Math heuristic methods that students can learn to master and apply when attempting problem sums.
The 12 Math Heuristic Method
1. Model Drawing:
This strategy involves drawing visual representations or diagrams to help students understand and solve word problems. By representing the problem visually, students can better visualize the relationships and identify the necessary mathematical operations.
2. Guess and Check:
This math heuristic method encourages students to make an initial guess or estimate and then check if their guess satisfies the conditions of the problem. If the guess is incorrect, students modify their guess until they find the correct answer.
3. Work Backwards:
In this approach, students start with the final outcome of a problem and work backwards step by step to determine the initial conditions or values. It helps students break down complex problems into smaller, more manageable steps.
4. Systematic Listing:
This math heuristic method involves creating a systematic list or table to organize information and possibilities. It helps students organize their thoughts and prevent overlooking potential solutions or combinations.
5. Make a Supposition:
Here it involves making an educated guess or supposition to simplify a problem. By assuming a value or condition, students can explore the problem and derive a solution more easily.
6. Look for Patterns:
This strategy encourages students to look for patterns or regularities in numbers, shapes, or operations. By identifying patterns, students can make predictions, generalize rules, and solve problems more efficiently.

7. Before-After Concept:
This math heuristic method is applied where the questions show there is a change resulting in a ‘before’ situation and an ‘after’ situation. One will need compare the two situations in order to understand the question fully and find a way to solve it. At best, the method is combined with the model drawing method (Number 1).
8. Act it Out:
This strategy requires pupils to visualize the content of the problem and what is entailed. Through the actions of what the problem says, they can come to a conclusion after that. The physical action makes the parts of the story sum and the relationship more vivid and real in the students’ minds. They may use physical objects or manipulatives to represent information. This skill is useful to introduce new concepts and to allow pupils to explore the concepts more meaningfully.
9. Table Drawing:
Some questions may ask students to identify the number of unique combinations present in a set of objects. Tables help to simplify word sums to help to figure out solutions. By creating a table with all the different variables and changing each variable one can arrive at the answer more easily. When doing guess and check (Number 2), constructing tables can prove useful.
10. Simplify:
Students can change the scenario given in questions to a simplified hypothetical scenario that can help them understand the problem better. This could be because the numbers and values in the question make it difficult to find the solution by merely reading the question.
For example:
The cost of 3 pens and 5 rulers cost $11. The cost of 6 pens and 9 rulers is $21. What is the cost of one pen?
You may start by simplifying the information.
Pens are represented by the letter P and rulers are represented by the letter R.
3P + 5R = $11—– Equation (1)
6P + 9R = $21 —– Equation (2)
We can turn Equation (1) into a new equation, Equation (3) by merely doubling.
6P + 10R = $22—– Equation (3)
Here the sum is more easily solved. This math heuristic method essentially simplifies and connects seemingly unrelated equations so that they make sense together, allowing students to look for the answer.
11. Solve Part of the Problem:
Solving part of a problem at time helps break up the job. More accuracy can come from this strategy and less confusion too. At the end, putting the parts together can help one solve the problem more easily.
Take the example below:
For example:
At a school library, each student could borrow up to 4 books. The bar graph below shows how many books students borrowed from the school library in one week. What was the total number of books borrowed from the library that week?
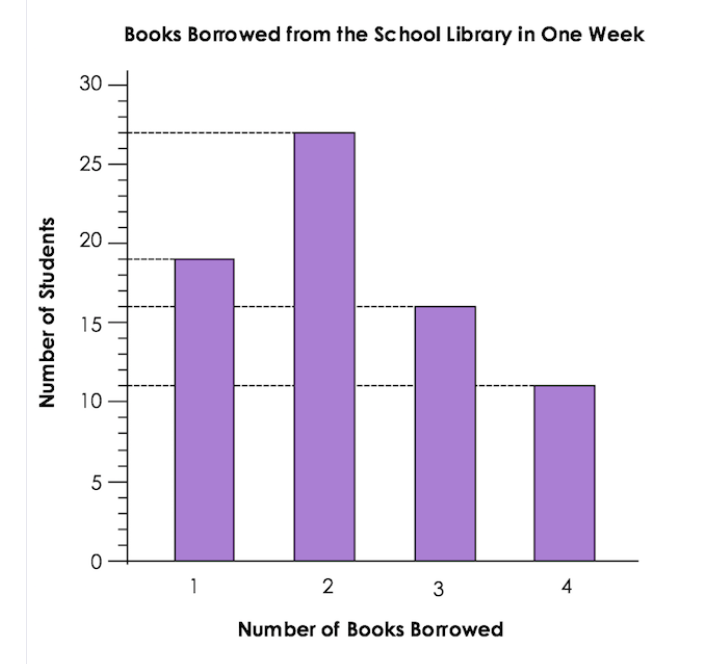
So, from the graph, one can solve each bar at a time.
19 students borrowed 1 book = 19 × 1 = 19 books
27 students borrowed 2 books = 27 × 2 = 54 books
16 students borrowed 3 books = 16 × 3 = 48 books
11 students borrowed 4 books = 11 × 4 = 44 books
The Answer: 19 + 54 + 48 + 44 = 165 books.
12. Restate the Problem:
By restating a problem in another way, pupils can view the problem in another perspective. One suggestion would be to use algebraic equations or expressions to represent and solve problems. It helps students translate word problems into mathematical equations, which can then be solved using algebraic techniques.
For the younger students the example below may help.
For example:
There are some identical pens and erasers. 2 pens and 3 erasers are 45 centimetres long altogether. 6 erasers and 2 pens are 60 centimetres long altogether. What is the length of 3 erasers?
So, if we subtract the total length of 2 pens and 6 erasers from that of 2 pens and 3 erasers, we get the length of 3 erasers.

60 cm – 45 cm = 15 cm
The length of 3 erasers is 15 cm.
Conclusion:
These math heuristic methods are not intended to be rigid rules, but rather flexible problem-solving techniques that students can apply to a variety of mathematical problems. By teaching and practicing these heuristics, the Singapore Math curriculum aims to develop students’ problem-solving skills and enhance their mathematical understanding.

At S.A.M. Hougang, our trainers act as guides and facilitators while our kids embark in the Singapore Math program. They coach and mentor our students, and ensure the class environment is one to promote thinking, self-expression and self-development. In this way, we are able to motivate the kids, boost their confidence and help them discover the joy and meaningfulness of learning mathematics.
